Нахождение НОД (наибольшего общего делителя) с помощью рекурсивной функции

Вычислить НОД с помощью рекурсии.

Наибольший общий делитель (НОД) чисел 3430 и 1365 – это 35. Другими словами, 35 – наибольшее число, на которое и 3430 и 1365 делятся без остатка. Чтобы убедиться в этом, разложим оба числа на простые сомножители:

3430 = 2 * 5 * 7 * 7 * 7
1365 = 3 * 5 * 7 * 13

и выделим пары общих сомножителей. В данном случае это пары 5 и 7. Наибольший общий делитель – это произведение совпадающих сомножителей; в данном случае это 5 * 7 = 35.

Более изящный метод поиска НОД – алгоритм Евклида. Найдем остаток от деления 3430 на 1365:

3430 mod 1365 = 700

Так как этот остаток не равен нулю, повторим то же действие, подставив вместо первого числа второе, а вместо второго – остаток:

1365 mod 700 = 665

Этот остаток также не нуль, поэтому еще одно деление:

700 mod 665 = 35

И еще одно:

665 mod 35 = 0

Теперь остаток – нуль, следовательно, НОД равен 35. Вот и отлично.

Следующая программа на Паскале использует метод Эвклида и рекурсию:

var a, b, c, answer: integer;
 
function gcd(m, n: integer): integer;
    var modulo: integer;
    begin
        modulo := m mod n;
        if modulo = 0 then
            gcd := n
        else
            gcd := gcd (n, modulo)
    end;
 
begin
    write('Enter two numbers: ');
    readln(a, b);
    if a < b then begin
        c := a;
        a := b;
        b := c;
    end;

    answer := gcd(a, b);
    
    writeln('Greatest common divisor: ', answer);
end.

Если представить, что в функцию сразу подставляются числа 665 и 35, то сразу ясно, как вычисляется gcd(665, 35): остаток modulo будет равен нулю и функция возвратит число 35 (ветка if). А вот при обращении gcd(3430, 1365) modulo будет равен 700, и, следовательно, функция вызовет себя еще раз в виде gcd(1365, 700). Таким образом, при каждом обращении Паскаль как бы создает новую копию функции gcd:

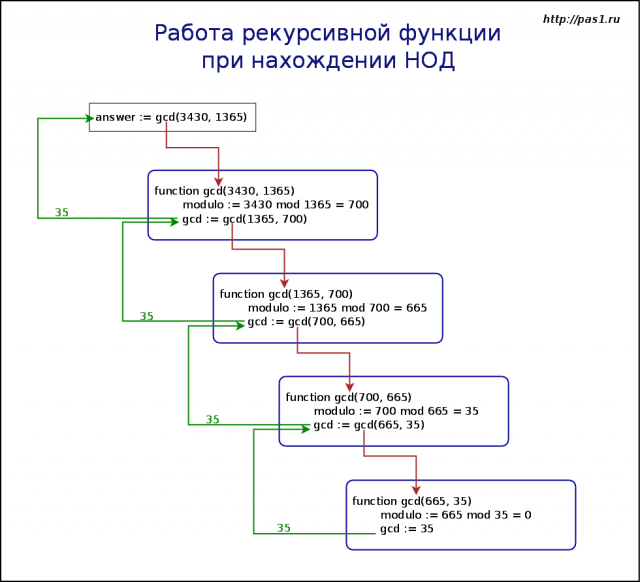
1. Из основной ветки программы вызывается функция gcd. Результат работы данной функции в дальнейшем будет присвоен переменной answer.
2. В функции gcd вычисляется остаток от деления чисел 3430 и 1365. Поскольку он не равен нулю, то осуществляется повторный вызов функции, но уже с числами 1365 и 700 (700 – это остаток от первого деления).
3. При третьем вызове функции передаются числа 700 и 665.
4. При четвертом – 665 и 35. Здесь остаток равен 0. Следовательно, результатом работы функции является число 35 (gcd = 35).
5. Результат четвертого вызова возвращается в третий.
6. Третий – во второй.
7. Второй – в первый.
8. Первый – в основную ветку программы и присваивается переменной answer.